vendredi 21 mai 2004, posté par AMAND Gilles

Black 2 courbes

Fichier au format excel de Gilles AMAND Lycée Val de Murigny REIMS

Ce fichier permet de visualiser sur un abaque Black Nichols deux courbes pour un système pouvant comprendre :

• un premier ordre
• un second ordre
• un integrateur pur
• un retard pur
• un filtre premier ordre
• un second ordre
• un correcteur :
  • PID mixte ou
  • PID série ou
  • PID parallèle

Outil precieux permettant de vérifier l’efficacité d’un correcteur puisque le correcteur peux être validé ou non sur chaque courbe et ainsi les comparer.

Ne pas hésiter à communiquer vos éventuelles corrections ou améliorations par le site à l’auteur.

ETUDE PLAN DE BLACK-NICHOLS

Gilles AMAND - REIMS

• Introduction :
  • L’utilisation du plan de Black permet d’étudier la stabilité d’un sytème bouclé par une méthode isochrone en traçant la fonction de transfert en boucle ouverte T(jw) d’un procédé en boucle ouverte.
  • Ce document n’est pas un cours sur les diagrammes de Black et des abaques de Nichols. L’essentiel du propos est constitué par un fichier écrit sous tableur vous permettant de tracer la représentation de deux fonctions de transfert. Chaque fonction de transfert peut être le produit de 2 fonctions fondamentales du premier ordre, de 2 fonctions fondamentales du second ordre, d’un temps mort, d’un correcteur PID (série, mixte ou parralèle). Afin de préserver la compatibilité entre les diverses versions d’Excel et afin de vous permettre d’enrichir assez facilement le produit, aucune macro n’a été utilisée.
  • L’étude fastidieuse de la stabilité est donc remplacée par la visualisation rapide des résultats obtenus. L’interprétation des courbes est presque immédiate avec un peu d’habitude.

• Quelques résultats importants sont rappelés :

• On étudie la stabilité du sytème en boucle fermée F, avec retour unitaire, à partir de la réponse isochrone du procédé en boucle ouverte T.

• Le plan de Black :

• La position de la courbe par rapport au point critique permet de déterminer la stabilité :

• STABLE :

  

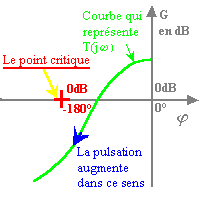
• JUSTE OSCILLANT :

  

• INSTABLE :

  

• La lecture des marges de phase et de gain permet de déterminer la robustesse :

  

• Action d’un correcteur :

  

• On étudie donc le produit C(jw).T(jw) dans le plan de Black

• Le déplacement de la courbe par l’action proportionnelle : K = coefficient d’action proportionnelle = "gain du régulateur", en fait du correcteur.

• K>1 et donc 20.log(K)>0 :

  

• K<1 et donc 20.log(K)<0 :

  

• Le déplacement de la courbe par l’action intégrale (PI avec K=1) :

Montée de tous les points et déplacement à gauche (plus important pour les faibles fréquences) ce qui implique une diminution de la robustesse (diminution de la marge de phase et de la marge de gain).

• Le déplacement de la courbe par l’action dérivée (PD avec K=1) :

Montée de tous les points donc diminution de la robustesse (diminution de la marge de gain).

Déplacement à droite plus important pour les fortes fréquences donc augmentation de la robustesse (augmentation de la marge de phase).

• Ces deux effets contraires au niveau de la stabilité impliquent un choix judicieux du temps d’action dérivée.

  

Les renseignements donnés par les abaques de Nichols :

• Les courbes en bleu sont les courbes isogain en boucle fermée.
• Les courbes en vert sont les courbes isophase en boucle fermée.

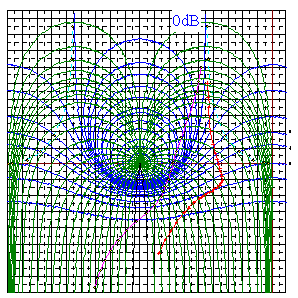
• Si le lieu de la fonction de transfert en boucle ouverte pénètre dans la zone où le gain est plus grand que 0 dB en boucle fermée c’est qu’il y a résonance ; c’est le cas pour la courbe en magenta. On peut alors déterminer la pulsation de résonance et, en assimilant la fonction de transfert à celle d’un système du second ordre, estimer le taux de dépassement.

• De nombreux réglages préconisés par Broïda ou par Ziegler et Nichols amènent la courbe représentative de la fonction de transfert en boucle ouverte à tangenter à l’abaque isogain en boucle fermée à 2,3dB ce qui entraîne souvent un dépassement important de l’ordre de 30%.

		ABAQUE BLACK Zip - 282.9 ko

[ Plan du site ] [ Haut ]