LES ASSERVISSEMENTS

 

 

1- Notions de systèmes asservis

  • 1-1 : Système non bouclé

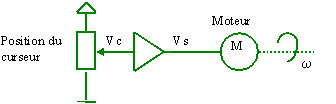
    Si l’on veut commander la vitesse d’un axe de moteur, il faut ceci :

    •

  • Il existe une relation entre la position du curseur et la vitesse de rotation w, soit w=a.Vc + b.

    Si l’on veut une certaine vitesse, comment peut-on être sûr qu’elle soit atteinte?, qu’elle soit stable au cours du temps? (Si l’on a une variation de l’amplificateur ou une variation du couple).

    Un tel système est dit NON BOUCLE.

    1-2 : Système bouclé (ou système à retour)

    La solution consiste à comparer la consigne de vitesse (Vc) avec une image de la vitesse réelle, soit le principe suivant :

    •

  • e est appelé écart ou erreur = Vc - Vr.

    Un tel système est dit BOUCLE.

    1-3 : Exemples

  • Vous êtes au volant de votre voiture et vous devez rouler à 90km/h; vous avez donc le regard sur votre compteur et le pied sur l’accélérateur. Pour avoir la vitesse constante vous disposez de deux informations :
  • Ø la vitesse réelle de la voiture;

    Ø la vitesse désirée.

    •

    Cette vitesse désirée est consignée dans le code de la route. Si le conducteur est idéal, nous aurons la vitesse de consigne égale à la vitesse réelle de la voiture.

    On note Vc (vitesse de consigne) et Vr (vitesse réelle).

    En réalité le conducteur module la puissance fournie par le moteur en fonction de l’écart entre Vc et Vr. Le conducteur compare Vc et Vr et cherche à rendre cet écart nul (noté e). On peut alors parlé de système asservi où la sortie est asservie à la valeur de l’entrée.

    Ø Donner d’autres exemples d’asservissements :

    •

    1-4 : Modélisation

    On peut modéliser l’exemple précédent comme ceci :

    •

  • Avec Vc : vitesse de consigne
  • Vl : vitesse lisible à la sortie du compteur
    •
  • On peut modéliser l’action de l’homme à une comparaison entre la vitesse Vc et la Vl soit :
    •

     

  • Si l’asservissement fonctionne correctement, Vc=Vr quelque soit Vc.
    •

    2- Qualité des systèmes asservis

  • On peut modéliser tous les systèmes asservis suivant ce modèle :
    •

  • 2-1 : Stabilité

    Calcul de Vs : Vs = A * e et e = Vc-Vr et Vr = B * Vs ce qui donne finalement : Vs/Vc = A/(1+A*B)

    La relation ci-dessus montre que si A*B tend vers -1, la sortie Vs tend vers l’infini : le système est alors INSTABLE.Un asservissement est stable si A*B>-1

    2-2 : Précision

    Le but d’un asservissement est que la sortie suive le plus fidèlement possible la consigne, soit e=0. Imaginons maintenant que vous êtes à l’arrêt sur le bord de l’autoroute, vous démarrez et votre consigne est de 130km/h. Si votre asservissement est correct, Vr=130km/h au bout d’un certain temps. Ceci est illustré ci-dessous :

    •

  • Courbe 1 : Vous avez trop accéléré et vous ralentissez pour atteindre la vitesse de consigne

    Courbe 2 : Vous êtes un fin conducteur car vous ne dépassez jamais la consigne de 130km/h, mais que de temps perdu (T2>>T1).

    Courbe 3 : Il existe dans ce cas une erreur sur la précision, le système ne peut suivre la consigne. Soit l’asservissement est mal calculé (conducteur défaillant) soit la puissance du moteur est insuffisante.

    •

    Erreur de précision : ep = lim(e(t)) = 0 avec t ® ¥ pour un asservissement correct.

  • 2-3 : Rapidité

    A l’aide des chronogrammes ci-dessous, on définit le temps de réponse comme étant le temps mis par la sortie pour atteindre la valeur de consigne à +/- 5%.

    •

     

  • 2-4 : Environnement du système

    Pour l’instant, nous n’avons pas considéré les action de l’extérieur sur le fonctionnement d’un système : ce sont les perturbations comme par exemple l’influence du relief sur la vitesse de notre voiture. Pour ce cas la modélisation devient :

    •

  • Remarque : Si l’asservissement est correct Vr doit être constant quelles que soient les variations du couple demandées.
    •

    3- Correction d’un système asservi

  • Pour respecter la stabilité, pour augmenter la précision et diminuer le temps de réponse, il est souvent nécessaire de placer dans la chaîne directe, un correcteur.

    La modélisation devient par conséquent :

    •

     

  • Il existe différents types de correction suivant les qualités voulues.

    3-1 : Correcteur proportionnel

    Le correcteur proportionnel est une multiplication par une grandeur K, réelle et supérieure à 1.

    •

    U = K * e

  • L’expression Vs/Vc devient :
    •

    Vs/Vc = AK/(1+AKB)

     

  • Remarques : - Si K est trop grand, l’erreur (éventuelle) sera augmentée et cela peut créer le phénomène d’instabilité.
  • - Dans l’autre cas (pas d’erreur) Us atteint plus rapidement la valeur de consigne Uc (meilleur précision).
    •

    • Conclusion : Il y aura donc un dilemme stabilité/précision; par conséquent il faut trouver un compromis entre ces deux paramètres. Comment ?

    En remarquant que :

  • Ø La précision concerne le régime permanent (fréquences basses);

    Ø La stabilité concerne le régime transitoire (fréquences élevées).

    è Il faut amplifier faiblement pendant le régime transitoire et d’avantage en régime permanent. Il faut donc réaliser un amplificateur à gain variable en fonction de la fréquence.

    •

  • Ceci se réalise soit :
  • è En augmentant le gain aux fréquences faibles, cette action est dite intégrale; c’est le principe des correcteurs PI (Passe Bas);

    è En réduisant le déphasage (entrée/sortie) aux fréquences élevées, cette action est dite dérivée; c’est le principe des correcteurs PD (Passe Haut).

    è En combinant ces deux types de correction; c’est le principe des correcteurs PID.

    •

    • 3-2 : Correcteur intégral

  • Pour un système sans intégration (dans la fonction de transfert), la correction proportionnelle laisse toujours subsister une erreur de précision. En effet si e était nulle KAe le serait aussi et le système ne serait plus alimenté.

    De plus lors d’une variation brusque de consigne, e est très grand, donc la sortie du correcteur se sature. Pour éviter ceci, on utilise une commande progressive de type intégrale (PB) :

    •

    où T1 est la constante de temps d’intégration
  • Si T1 est trop petit, U croit trop vite sans laisser le temps au système de réagir.

    Si T1 est trop grand, U croit trop lentement et le démarrage est lent.

    Effets : - Annule l’erreur de précision.

  • - Cette commande est progressive mais persévérante, ce qui diminue la rapidité.

    • Exemple :

    		  

     

    3-3 : Correcteur dérivé

  • Exemple : Lorsque vous voulez maintenir la vitesse de votre voiture constante, malgré le relief de la route, vous surveillez votre compteur :
  • Ø Si la vitesse a tendance à diminuer, vous accélérez.

    Ø Si la vitesse a tendance à augmenter, vous relâchez l’accélérateur.

    •

    • A la moindre variation de vitesse, suivant son sens, vous agissez en conséquence, en anticipant presque la correction nécessaire.

    Le sens de toute variation peut être donné par le dérivée :

    •

    U = td*de /dt

    		 où td est la constante de temps de dérivation

    La correction dérivée est toujours associée à une correction proportionnelle :

    U = K*[e(t) + td*de/dt]

    		  
  • Effets : - Augmente la rapidité.
    •

    - Augmente la stabilité.

    Exemple :

    		  

     

  • 3-4 : Exemple de correcteur PID
    •

     

    4- Différents asservissements

  • On distingue deux grands types d’asservissements en fonction de la technologie employée.

    4-1 : Les asservissements analogiques

    Toutes les fonctions (comparaison, correction, ...) traitent des tensions analogiques. Elles sont généralement à base de composants discrets R, C et d’AIL. La correction peut être parfois traitée numériquement (ordinateur, mp, ...).

    •

  • 4-2 : Les asservissements numériques

    Toutes les fonctions sont réalisées numériquement. La correction sera alors programmée.

    •

     

  • 4-3 : Choix des asservissements

    Pour des systèmes lents, les constantes de temps sont grandes et les valeurs des composants discrets ne suffisent plus ® asservissement numérique.

    Lorsque le correcteur doit s’adapter pour la commande des différents processus ® asservissement numérique.

    Lorsque l’asservissement commande un processus rapide ® asservissement analogique.

    •

    retour accueil lycée  retour accueil  retour cours ssi

    Document html par Franck Robichon