Le pont de VOIGT.

Dans ce qui précède nous avons supposé l'existence de dispositifs transformant l'accélération de la membrane en une tension électrique. Le plus ancien est le pont de VOIGT qui transforme la vitesse de la membrane en une tension électrique. Il suffit après de le faire suivre d'un étage qui fait la dérivée pour avoir une tension proportionnelle à l'accélération. Ce dernier est tout simplement un circuit $C,R$ de type filtre passe-haut du premier ordre utilisé très en dessous de sa fréquence de coupure. Voir le paragraphe 2.9 : la fonction de transfert est

$$H(j.\omega)=\frac{j\omega/\omega_0}{1+j\omega/\omega_0}$$

Si $\omega \ll \omega_0$ le dénominateur est voisin de l'unité et la fonction de transfert se réduit à $j\omega/\omega_0$. Or on sait que multiplier par $j\omega$ dans le domaine complexe revient à dériver par rapport au temps dans le domaine temporel.

Comme tous les ponts le pont de VOIGT est constitué de quatre dipôles: dans l'une des branches on trouve bien évidemment le haut-parleur défini par son impédance de la bobine bloquée $Z_b$ et le produit $B.l$. Comme on se trouve aux basses fréquences on pourra considérer que l'impédance bloquée est la mise en série de la résistance $R$ de la bobine et de son inductance propre $L$. La branche voisine a pour valeur $\alpha .Z_b$ avec $\alpha<1$, c'est donc la mise en série d'une résistance $\alpha .R$ et d'une inductance propre $\alpha .L$. Cet ensemble est traversé par le courant fourni par l'amplificateur, c'est pour cela que le circuit auxiliaire ne doit pas consommer trop de puissance. On choisit en général $\alpha$ voisin de $0,2$.

L'autre partie du pont est constituée par la mise en série de deux résistances $R_1$ et $\alpha .R_1$ de valeurs assez supérieures à celle du haut-parleur pour ne pas prélever trop de puissance à l'amplificateur.

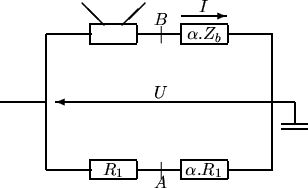
La partie du bas est un diviseur potentiométrique à résistances tel que : $U_A=U.\alpha /(1+\alpha)$. On reste toujours en notation complexe et on désigne par $V$ l'amplitude complexe de la vitesse de la bobine mobile et par $I$ le courant qui traverse cette bobine. La tension aux bornes du haut-parleur vaut $B.l.V+Z_b.I$. On peut calculer $I$ grâce à l'autre branche du pont : $I=U_B/\alpha .Z_b$. Ce qui donne $U-U_B=B.l.V+U_B/\alpha$ ou encore $U_B.(\alpha +1)/\alpha=U-B.l.V$. Il vient enfin $U_A-U_B=U.\alpha/(\alpha+1)-U.\alpha/(\alpha +1)+B.l.V.\alpha/(\alpha+1)$ soit

$$U_A-U_B=\frac{B.l.\alpha}{\alpha+1}.V$$

La vitesse est donc bien proportionnelle à la différence de potentiel $U_A-U_B$. On constate que cette différence est flottante par rapport à la masse, il y donc lieu d'utiliser un amplificateur de différence pour ramener une tension finale avec une référence à la masse de façon à éviter les problèmes.

Cette tension alimente ensuite le circuit $C,R$ pour obtenir la dérivée par rapport au temps et ainsi une tension proportionnelle à l'accélération.

Dans certains cas on peut avoir besoin d'asservir la vitesse lors de la propagation d'une onde sonore dans un tuyau. Le problème est alors délicat car on doit asservir une résonance. On aura donc de la peine à obtenir une courbe de réponse plate.